
 Electric Fieldوقوانينه وتعريفه
Electric Fieldوقوانينه وتعريفه----------------------------------------
Electric field is defined as the
electric force per unit charge

------------------------------------------------------
Electric Field of Point ChargeThe electric field of a point charge can be obtained from Coulomb's law: 
The electric field from any number of point charges can be obtained from a vector sum of the individual fields. A positive number is taken to be an outward field; the field of a negative charge is toward it.

*******************
Electric Field of Point Charge
The
electric field of a point charge Q can be obtained by a straightforward
application of Gauss' law. Considering a Gaussian surface in the form of a sphere at radius r, the electric field has the same magnitude at every point of the
sphere and is directed outward. The electric flux is then just the electric field times the area of the sphere.
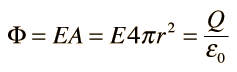
The electric field at radius
r is then given by:
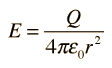
If another charge
q is placed at
r, it would experience a force
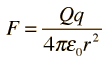 so this is seen to be consistent with Coulomb's law.
so this is seen to be consistent with Coulomb's law. **********************
Electric Field of Conducting Sphere
The
electric field of a conducting sphere with charge Q can be obtained by a straightforward application of
Gauss' law. Considering a Gaussian surface in the form of a sphere at radius r > R , the electric field has the same magnitude at every point of the surface and is directed outward. The electric flux is then just the electric field times the area of the spherical surface.
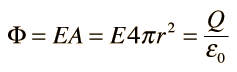
The electric field is seen to be identical to that of a point charge Q at the center of the sphere. Since all the
charge will reside on the conducting surface, a Gaussian surface at r< R will enclose no charge, and by its symmetry can be seen to be zero at all points inside the spherical conductor

************************
Electric Field: Sphere of Uniform Charge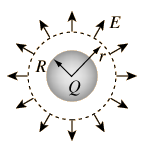 The electric field of a sphere of uniform charge density and total charge charge Q can be obtained by applying Gauss' law. Considering a Gaussian surface in the form of a sphere at radius r > R, the electric field has the same magnitude at every point of the surface and is directed outward. The electric flux is then just the electric field times the area
The electric field of a sphere of uniform charge density and total charge charge Q can be obtained by applying Gauss' law. Considering a Gaussian surface in the form of a sphere at radius r > R, the electric field has the same magnitude at every point of the surface and is directed outward. The electric flux is then just the electric field times the area of the spherical surface.
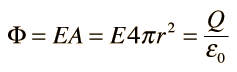
The electric field outside the sphere (
r > R)is seen to be identical to that of a point charge Q at the center of the sphere.
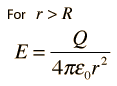
For a radius
r < R, a Gaussian surface will enclose less than the total charge and the electric field will be less. Inside the sphere of charge, the field is given by:

***********************
Inside a Sphere of Charge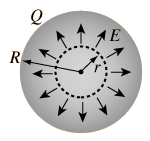 The electric field inside a sphere of uniform charge is radially outward (by symmetry), but a spherical Gaussian surface
The electric field inside a sphere of uniform charge is radially outward (by symmetry), but a spherical Gaussian surface would enclose less than the total charge Q. The charge inside a radius r is given by the ratio of the volumes:
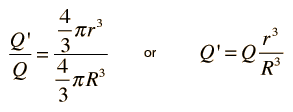
The
electric flux is then given by
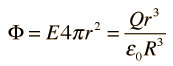
and the electric field is
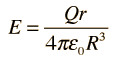
Note that the limit at r= R agrees with the expression for r >= R.
************************
وأخيرا مع الثوابت
Electric and Magnetic Constants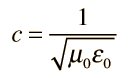
This gives a value

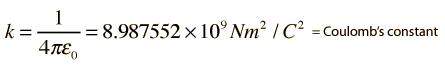
********
Enjooooooooooy 



