أدوات القياس الكهربائية
مقدمة في علم القياس
القياس عملية فيزيائية تعتمد على التجربة العلمية التي تقارن بين مقادير يُراد قياسها وأخرى مرجعية من جنسها فيزيائياً تُسمى واحدات القياس.
ويؤدي علم القياس metrology دوراً رئيساً في تطور العلوم النظرية والتقنية. ومن أهدافه الأساسية استنتاج النظريات التي تكشف عن القوانين المعبرة كمياً عن القيم المختلفة.
وتجرى عملية القياس بتقنيات متنوعة إلكترونية أو كهربائية أو ميكانيكية أو غيرها. وتعد التقنيات الكهربائية والإلكترونية أكثرها انتشاراً في جميع المجالات العلمية بسبب تميزها بالدقة والحساسية العاليتين وسرعة النتيجة وإمكان تنظيم المعلومات وتنسيقها وتحليلها إضافة إلى إمكان القياس عن بعد.
وأدى التطور الكبير في تقنيات الهندسة الكهربائية والإلكترونية إِلى ظهور أجهزة قياس مركبة يمكنها أن تقيس مقادير كهربائية وغير كهربائية من ميكانيكية وحرارية وحيوية وغيرها وأن تحلل نتائجها وتنسق بين مؤثراتها وتنظِّم معلوماتها. فأجهزة القياس «الذكية» مثلاً مكونة من عدة وسائل تُربط بحسب نظام معين وتؤلف منظومة القياس.
وهناك حتى اليوم طريقتان أساسيتان في القياس:
الطريقة المباشرة والطريقة غير المباشرة.
أما الطريقة المباشرة فتتميز بخاصة القياس التي يُحصل فيها على النتيجة فوراً عند تأثير المقدار المجهول في دخل الجهاز أو المنظومة، وهي تنقسم، بحسب التقنية المستخدمة في إظهار النتيجة، إلى الطريقة التمثيلية analogue method والطريقة الرقمية digital method.
أما الطريقة التمثيلية فتتميز بعلاقة معروفة بين مقداري دخل الجهاز وخرجه فيكون هذان ممثّليْن توابع زمنيةً مستمرةً (غير منقطعة) أي أنهما متماثلان.
وأما الطريقة الرقمية فتتميز بعلاقة ربط معروفة بين قيمتي دخل الجهاز وخرجه إلا أن مقدار الخرج تابع زمني منقطع أي إِن إشارة الخرج منقطعة زمنياً وتعطي النتائج أرقاماً على لوحة إظهارها.
وأما في الطريقة غير المباشرة، فعند تأثير المقدار الفيزيائي المراد قياسه فإن الجهاز لا يعطي النتيجة فوراً وإنما يقارنه مع القيم المعيارية، ويجري حساب المقدار المجهول بوساطة علاقة تربط بين القيم ربطاً غير مباشر، ومن أهمها طريقة المقارنة التي تقوم على أسلوب التبديل substitution method أي بمبادلة المقدار المجهول بآخر معلوم بعد مقارنة كل منهما إفرادياً بالمعيار، أو على الأسلوب الصفري null method الذي يعتمد على المقارنة بالمقدار المجهول والمعايير في آن واحد حتى الحصول على صفر جهاز المقارنة أي مساواة الأول والثاني ويسمى عادة بحالة التوازن، ويسمى جهاز المقارنة هذا عادة بالكاشف الصفري null detector. ولكن لا يمكن في بعض الحالات التوصل إلى التوازن الكامل، لذلك يقاس الفرق الأصغري بينهما وتسمى بالطريقة التفاضلية، أما جهاز الكاشف فيسمى في هذه الحالة بكاشف الخطأ error detector.
وتتأثر عملية القياس بالشروط المحيطة من درجات الحرارة والرطوبة والمؤثرات الفيزيائية الخارجية. ويراعى، لتوفير الدقة في عملية القياس، أن تتم هذه العملية في الشروط النظامية التي تحددها الأنظمة المعتمدة في الدولة أو النظم الدولية.
وأجهزة القياس الكهربائية هي وسائل تقنية إشارة دخلها كهربائية. وهي تقارن بين القيم المجهولة المراد قياسها والقيم المعيارية المعتبرة بعلاقة ربط معروفة بين إشارتي الدخل والخرج، وتتعين اعتماداً على النظرية الديناميكية الكهربائية أي بتأثير الطاقة الكهربائية، وأبسط أشكالها تسمى المقاييس الكهربائية، وقد تتألف من عدة تجهيزات قياس، ومنها وسائل التحسس وغيرها، لتكوّن منظومة قياس مستقلة قادرة على التحكم في عملية القياس وتنظيمها ومراقبة القيم المختلفة.
ومن أجهزة القياس الكهربائية:
أجهزة القياس المقارنة، وأجهزة القياس الرقمية، وأجهزة القياس التمثيلية، وفي الأخيرة يكون مقدار الدخل الكهربائي تابعاً زمنياً مستمراً مماثلاً لتابع الخرج المتواصل زمنياً. وهي تصنف، بحسب طريقة إظهار النتيجة، في أجهزة القياس التمثيلية ذات المؤشر وأجهزة القياس التمثيلية لرسم الاهتزاز. وتضم الأولى جميع أجهزة القياس التي تدل على النتيجة الواحدة بوساطة مؤشر ميكانيكي أو شعاع ضوئي، وأغلبها كهربائية ميكانيكية، لذلك تسمى أجهزة القياس الكهرميكانيكية ذات المؤشر. وهذه الأخيرة تنقسم إلى مجموعات بحسب النظرية الكهرمغنطيسية المعتمدة في مبدأ عملها، أي تحويل الطاقة الكهربائية إلى ميكانيكية مكافئة ومعيرة بزاوية انحراف المؤشر على لوحة «إظهار النتيجة». ومن هذه المجموعات: أجهزة القياس ذات الوشيعة المتحركة وأجهزة القياس ذات النواة المتحركة وأجهزة القياس الكهرديناميكية وأجهزة القياس التحريضية وأجهزة القياس الكهرساكنة وأجهزة القياس الكهرحرارية.
أما أجهزة القياس التمثيلية لرسم الاهتزاز فيسمى واحدها اختصاراً «راسم الاهتزاز» (راسم الإشارة) oscillograph وهو جهاز تمثيلي يظهر على شاشته المنحني الزمني الممثل للتابع الرياضي المستمر للمقدار الكهربائي المراد دراسته والمؤثر في دخله.
ويصنف راسم الاهتزاز بحسب التقنية المعتمدة في إظهار منحني الإشارة إما في راسم الاهتزاز الضوئي الذي يعمل وفق مبدأ الشعاع الضوئي أو في راسم الإشارة المهبطي الذي يعمل بوساطة شعاع إلكتروني مولد من مدفع إلكتروني أو بوساطة صمام أشعة مهبطية.
وتقسم أجهزة القياس الكهربائية، بحسب المقدار الكهربائي الذي تقيسه، إلى: مقياس الأمبير am meter ومقياس الفولط voltmeter ومقياس الاستطاعة wattmeter ومقياس التردد frequency meter ومقياس الأوم ohm meter ومقياس الطاقة energy meter ومقياس عامل الاستطاعة power factor meter ومقياس التحريض المغنطيسي (تسلامتر) Tessla meter ومقياس التدفق المغنطيسي (السيالة المغنطيسية) flux meter وغيرها.
ومن المقاييس ما يقيس النسبة بين قيم مجهولة وأخرى عيارية معلومة فتسمى المقاييس التناسبية logometer. ومنها ما يقيس القيم الكهربائية الدقيقة (الصغيرة جداً) فيسمى المقاييس الغلفانية galvanometer. وجميع أجهزة القياس يمكن أن تقيس قيماً آنية أو حسابية أو قيماً وسطى أو فعالة، كما يمكن أن تقيس تكامل القيم في زمن معين مثل الشحنة الكهربائية والطاقة الكهربائية وتسمى أحياناً المقاييس التكاملية integrating instruments.
أجهزة القياس ذات الوشيعة المتحركة
هي مقاييس كهرميكانيكية تمثيلية ذات مؤشر ميكانيكي أو بقعة ضوئية تؤخذ نتائجها من لوحة مدرجة ومقسمة بحسب نظام وحدة القياس الدولية.
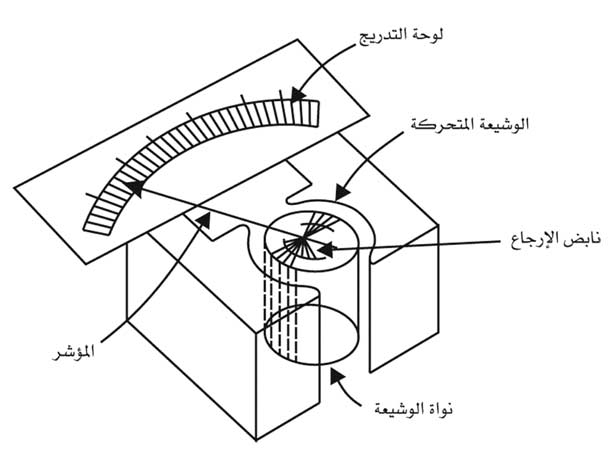(الشكل -1) مقياس كهربائي ذو وشيعة متحركة
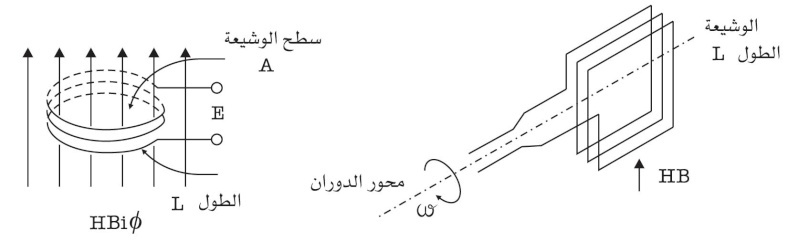
وتعتمد المقاييس ذات الوشيعة (الملف) المتحركة في مبدأ عملها على التأثير المتبادل بين الحقل المغنطيسي لمغنطيس دائم والحقل المغنطيسي لتيار مستمر يمر في وشيعة ملفوفة حول نواة حديدية ذات نفوذية مغنطيسية عالية (الشكل1).
ومن نتائج التأثير المتبادل بين المغنطيس الدائم والوشيعة حدوث مزدوجة من القوى المغنطيسية تؤدي إلى نشوء عزم يؤثر في الوشيعة المرتكزة على محور الدوران مما يؤدي إلى انحراف مؤشر الجهاز على اللوحة المدرجة. ويتعين عزم الفتل torque moment أو عزم القياس في الوشيعة المتحركة من العلاقة: Ms= 2rl.N.B.I حيث r نصف قطر الوشيعة و l طولها و N عدد لفاتها و B التحريض المغنطيسي في فجوة المغنطيس الدائم و I التيار الكهربائي المار في الوشيعة.
ويتم التوازن الستاتيكي في الجهاز عندما يتساوى عزم الفتل مع عزم نابض الإرجاع أو خيط الفتل في الجهاز، ويتحدد هذا التوازن من جداء زاوية الانحراف في ثابت نابض الإرجاع، وعند توازنهما يستنتج أن زاوية الانحراف تتناسب طرداً وخطياً مع التيار الكهربائي المار في الوشيعة باعتبار أن بقية المعاملات المشاركة تمثل ثوابت تصميمية داخل الجهاز.
ويتميز هذا المقياس بأنه يقيس التيارات الصغيرة بدقة عالية، وتتناسب زاوية القياس فيه مع شدة التيار، إلا أن هذا المقياس غير قادر على قياس التيار المتناوب قياساً مباشراً لأن القيمة الوسطى الحسابية لعزم الفتل فيه تساوي الصفر.
ولمقاييس الوشيعة المتحركة صفةٌ إيجابيةٌ أخرى مهمة هي التخامد الطبيعي المعتمد على نظام عملها، أي عندما تدور الوشيعة داخل الحقل المغنطيسي فإنه، بحسب معادلة مكسويل، ستتحرض قوة محركة كهربائية في وشيعة الجهاز. ولما كانت الدارة الكهربائية مغلقة عند عملية القياس، فإن تياراً كهربائياً معاكساً للتيار المراد قياسه سيمر في الدارة بحسب قاعدة لنز مما يؤدي إلى نشوء عزم مشابه لعزم الفتل يؤدي إلى تخامد الحركة الاهتزازية داخل الجهاز. وتنتمي غالبية المقاييس الغلفانية ومقاييس الأمبير والفولط الكهرميكانيكية إلى المجموعة ذات الوشيعة المتحركة بسبب مميزاتها المذكورة آنفاً حتى في مجال قياس القيم الحسابية الوسطى والعظمى والفعالة للتيار المتناوب الذي يُقوَّم أولاً ثم يقاس بوساطة جهاز الوشيعة المتحركة.
وإن أجهزة القياس ذات الوشيعة المتحركة تأخذ بالحسبان تأثيرات جميع العزوم ومنها عزم العطالة للأجزاء المتحركة وعزم التخامد الذي أشير إليه وكذلك عزم الاحتكاك، إلا أن هذا الأخير يهمل عادةً بسبب صعوبة حساباته لعدم تقيده بعلاقات معروفة.
وعند استخدام أجهزة الوشيعة المتحركة لقياس التيارات والتوترات العالية نسبياً يُستفاد من المخمدات الاصطناعية الميكانيكية أو المغنطيسية. وتتأثر المقاييس ذات الوشيعة المتحركة جميعها بالحقول المغنطيسية وبتغيرات درجة الحرارة والرطوبة والصدمات الميكانيكية.
مقياس الأمبير: إن إشارة الدخل الكهربائية في جميع المقاييس ذات الوشيعة المتحركة هي التيار الكهربائي، كما في علاقة عزم القياس. وتعمل مقاييس الأمبير بمقاومة داخلية تتعين من مقاومة ناقل الوشيعة والمقاومة الإضافية لتحقيق استقرار درجة الحرارة في أثناء عملها. والمقاومة الداخلية هي بوجه عام مقاومة صغيرة مما يزيد من أفضليات هذه الأجهزة في قياس التيارات الكهربائية، وإن درجة دقتها يمكن أن تصل إلى 0.1 وهي أعلى درجة دقة للأجهزة الكهرميكانيكية، ويدخل في هذه المجموعة من المقاييس مقاييس الأمبير والملّي أمبير والمكروأمبير وهي مقاييس تربط على التسلسل مع الأحمال المراد قياس تياراتها وذلك واضح من مبدأ عمل الجهاز.
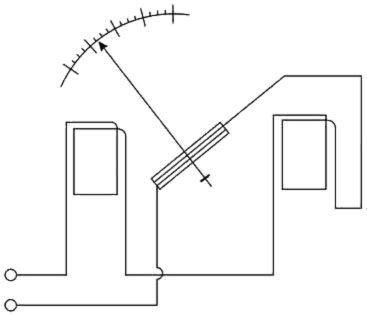
(الشكل 2) تغيير مجال القياس لمقياس الأمبير باستعمال مقاومات على التفرع وإن مقاييس الأمبير ذات الوشيعة المتحركة يمكن تغيير مجال قياسها بسهولة بوساطة مقاومات أومية (مفرِّعات shunts) تربط على التفرع مع المقاييس كما في الشكل 2 لأن المقاومة الكهربائية التفرعية ذات القيمة القياسية المعروفة تَقْصر الجهاز، وعندئذ، إذا أشار الجهاز إلى التيار i كان التيار الذي يجتاز الدارة مساوياً I، وهو أكبر من i بـn مرة (عامل الضرب):
وإذا كانت g هي المقاومة الداخلية للجهاز، وR المقاومة الموصولة على التسلسل مع g (تفادياً لتخامد الوشيعة الشديد) وs مقاومة المُفرِّعة، فإنه من السهل التوصل إلى أن
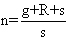
ومن الواضح أنه يمكن تغيير قيمة n بسهولة وذلك بتغيير قيمة s
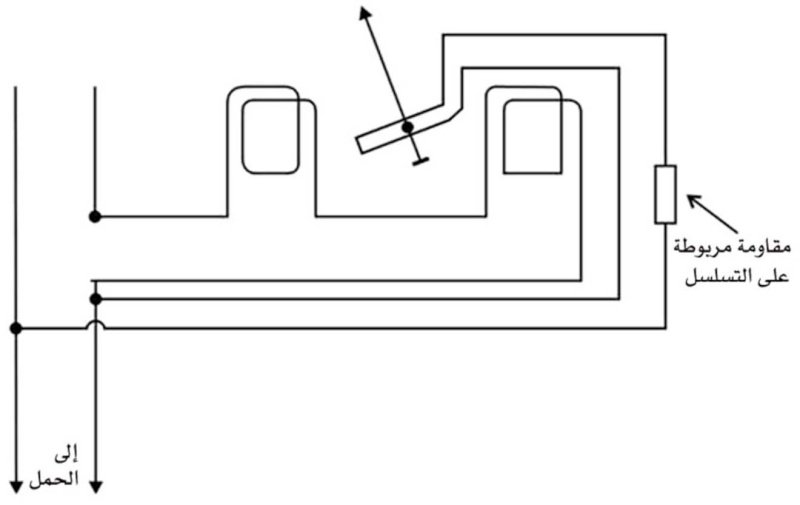
مقياس الفولط: يحوَّل مقياس الأمبير، ذو المقاومة الداخلية r، إلى مقياس الفولط بوَصْله على التسلسل مع مقاومة كبيرة R ويوصل مقياس الفولط دائماً على التفرع بين مربطي قطعة الدارة (الحِمْل) المراد قياس الفولطية voltage (التوتر) بينهما. ولجعل خطأ القياس صغيراً يجب أن تكون مقاومة مقياس الفولط الداخلية (أي r+R) أكبر بكثير من مقاومة الحمل.
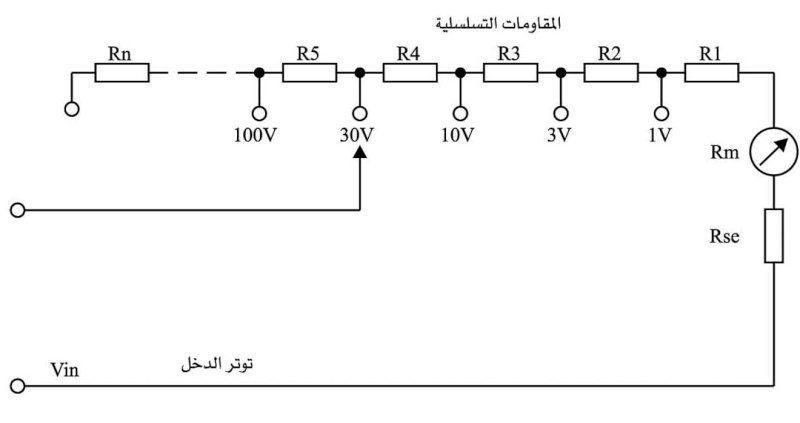(الشكل -3) المقاومات التسلسلية
ويُوسَّع مجال مقياس الفولط بوساطة مقاومات تسلسلية تربط مع الجهاز كما في الشكل 3 ويمكن بسهولة استنتاج قيم المقاومات التي توفر مجالات القياس المطلوبة اعتماداً على نظريات الدارات الكهربائية المعروفة.
المقياس الغلفاني: تسمى أدوات القياس التي تقيس قيماً دقيقة بالمقاييس الغلفانية، ولقد أثبتت التجربة الهندسية والقياسية أن المقاييس ذات الوشيعة المتحركة تعد أكثر ملاءمة لتصميم نماذج المقاييس الغلفانية.
وتصنف المقاييس الغلفانية في أصناف عدة بحسب القيم التي تقيسها، فمثلاً مقاييس المكرو أمبير، التي تقيس تيارات من مرتبة 10-6A أمبير وأقل، تمثل مقاييس غلفانية عادية، في حين أن المقياس الغلفاني المخصص لقياس تيارات من مرتبة 10-9A أمبير وأقل، ومن ثم يقيس النبضة الكهربائية، يسمى المقياس الغلفاني القذاف البالستي، وهو مقياس تكاملي أي يقيس تكامل نبضة التيار الكهربائي في زمن مروره في وشيعة المقياس، أي يقيس الشحنة الكهربائية التي اجتازته.
ويُسمى المقياس الغلفاني المخصص لدراسة الاهتزازات بالمقياس الغلفاني الهزاز الذي يستخدم في اتجاهين أساسيين في القياسات الكهربائية، ففي الاتجاه الأول يستخدم مقياساً كاشفاً في الدارات القياسية، ويعتمد على ظاهرة التجاوب (الطنين) بين ترددات التيار المتناوب والاهتزازات الحرة لذلك كثيراً ما يسمى المقياس الغلفاني المتجاوب أو التجاوبي.
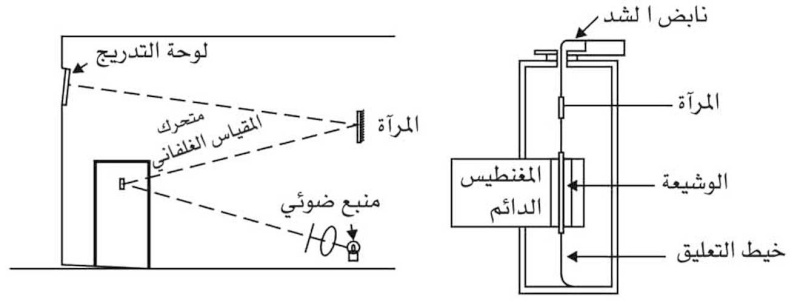(الشكل -4) مخطط المقياس الغلفانيأما الاتجاه الآخر فيعتمد على استخدام النظرية الاهتزازية للمقاييس ذات الوشيعة المتحركة الغلفانية في رسم الاهتزازات عندما يكون تردد التيار أصغر من تردد الاهتزاز الحر للوشيعة. وتتصف المقاييس الغلفانية بميزة مهمة هي الحساسية العالية وقياس القيم الدقيقة، لذلك فإن جميع محدداتها ومعاملاتها التصميمية والاستثمارية تخضع لعملية اختيار تصميمي بحيث تحقق الخصائص المذكورة آنفاً ومن أهمها العطالة المنخفضة وعزم الإرجاع الصغير. ويمكن أن يتحقق ذلك باستخدام خيط ذي عزم فتل صغير جداً والاعتماد على الأشعة الضوئية التي تؤدي إلى إظهار بقعة ضوئية على لوحة تدريج المقياس (الشكل 4).
ولقد أثبتت التجربة الهندسية أن المقاييس الغلفانية العادية تتميز بحساسية ثابتة غير تابعة للحركة الاهتزازية ولكنها تؤثر تأثيراً مباشراً في زمن التخامد ومن ثم في زمن القياس. وكذلك يمكن أن تؤدي إلى أخطاء فادحة بحسب نوع الحركة، ويتوقف ذلك على العلاقة بين المقاومة الداخلية للجهاز والمقاومة المكافئة الخارجية لدارة القياس المغلقة، وعند مراعاة أن معامل درجة التخامد في داخل هذه الأجهزة يجب أن يساوي تقريباً الواحد للحصول على أصغر زمن للتخامد واستقرار زاوية الانحراف استقراراً مضموناً فإن المقاومة الخارجية يجب أن تساوي مقداراً يسمى المقاومة الخارجية الحرجة، وهو محدد أساسي للجهاز مكتوب على لوحته المرافقة، ولهذه الأسباب تستخدم مع المقاييس الغلفانية مقاومات على التفرع كما في الشكل 2 لتبقى المقاومة المكافئة الخارجية عند القياس ثابتة.
وإن المعامل الأساسي للمقياس الغلفاني هو حساسيته S بالنسبة للتيار أو التواتر
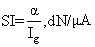
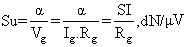
حيث: α زاوية انحراف الجهاز، Rg مقاومة وشيعة المقياس، Vg وIg التيار المار في الوشيعة والتوتر المطبق على مربطيه.
وإذا فرض أن المقاومة الكهربائية للدارة خارج مربطي المقياس الغلفاني هي RD، وأن المقاومة التي تحقق معامل درجة التخامد تساوي الواحد β=1 هي RDK فإن معامل درجة التخامد لهذه الأخيرة يتعين من العلاقة:
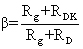
وهي علاقة مختصرة ومهمة في دراسات الحركات الاهتزازية وعملية القياس في المقاييس الغلفانية، وعادة عند استثمار هذا النوع من المقاييس الغلفانية فإن معامل درجة التخامد يجب أن يكون مساوياً الواحد تقريباً، أو أن تكون المقاومة الخارجية تقريباً مساوية للقيمة الحرجة.
ويتضح مما سبق أنه عند اختيار مقياس غلفاني للتيار يُنطلق من الأساسين العمليين التاليين:
ـ إذا كانت المقاومة المكافئة للدارة الخارجية RD عالية يُختار مقياس غلفاني بمقاومة RDK أعلى ما يمكن، ويجب أن تكون هذه المقاومة قريبة من المقدار RD لتوفير أعلى حساسية للمقياس فيما يخص التيار.
ـ إذا كانت المقاومة المكافئة للدارة الخارجية RD صغيرة يُختار مقياس غلفاني بحساسية عالية بالنسبة للتوتر ومقاومة إخماد حرجة صغيرة تساوي تقريباً المقاومة الخارجية.
ويعتمد المقياس الغلفاني القذاف (البالستي) في مبدأ عمله على الحركة القذفية لوشيعته عند مرور نبضة تيار صغير جداً، ويتناسب الانحراف القذفي طرداً مع شحنة التيار الكهربائية. وتتصف هذه المقاييس بدور period كبير للحركة الاهتزازية الحرة بالمقارنة بزمن نبضة مرور التيار، ويتم التوصل إلى ذلك بزيادة ثابت عطالة الجهاز، ويتميز المقياس الغلفاني القذاف بحساسيته العالية، إذ يتوقف مقدار هذه الحساسية على نمط الحركة الاهتزازية التي تؤديها الوشيعة أو البقعة الضوئية عند الانحراف. لذلك فإن عدم الالتزام بالمقاومة الحرجة لا يسبب مشاكل في عملية التخامد فقط وإنما في قيمة القياس أيضاً. وبتعبير آخر فإن المقياس الغلفاني القذاف يدرج لكل دارة قياس بحسب مقاومته المكافئة أو يعاير بحسب محددات الدارة الخارجية.
وتتميز مقاومات التفريع في المقاييس الغلفانية بوظائف عدة بحسب الهدف التصميمي للمقياس، فمن المقاييس مباشرة، ما يستعمل كاشفاً صفرياً في جسور التيار المستمر وفي مجزئات التوتر المستمر، ومنها ما يستعمل مقياساً مباشراً للشحنة الكهربائية، ومنها كذلك ما يستعمل لقياس المقادير المغنطيسية وغيرها.
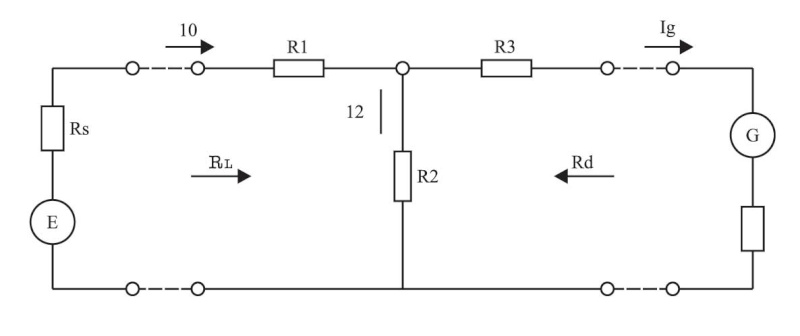(الشكل -5) المقياس الغلفاني القذاف ودارة الربط التابعة لهوإن مهام مقاومات التفريع كثيرة منها تأثيرها في العلاقة بين المقاومة الداخلية والخارجية ومن ثم في سير العملية القياسية مباشرة، ومنها حماية المقاييس الغلفانية من التيارات والتوترات الزائدة، إذ تربط معها على التفرع أو التسلسل، كما أن مقاومة التفريع تستخدم لمعايرة المقاييس الغلفانية أي تعيين حساسيتها وثابت قياسها (مقلوب الحساسية)، وبقية معاملات الجهاز. ولقد تبين بالتجربة أن المقاومات الكهربائية (R1,R2,R3) التي تربط مع المقياس (الشكل5) هي أفضل الاحتمالات الملائمة لخصائص الجهاز ودارة القياس لأنها توفر جميع المهمات المشار إليها سابقاً.
وتشكل هذه المقاومات دارة تخامد الإشارة في المقياس وتتعين قيمها من المبادئ الأساسية التي يعتمد عليها المقياس الغلفاني القذاف وهي أن تقوم بتفريع التيار بنسبة محددة بدقة لتساوي المقاومة المكافئة الخارجية Rd المقاومة الحرجة Rdc، وكذلك فإن المقاومة المكافئة للمفرعة وللمقياس الغلفاني يجب أن تكون معروفة تماماً وتمثل المقاومة المكافئة على خرج منبع القوة المحركة الكهربائية RL وهي تتعين من استطاعة الإشارة الكهربائية، فإذا كانت هذه الاستطاعة عالية نسبياً فيجب أن تكون المقاومة المكافئة الأخيرة مساوية للمقاومة الداخلية في المقياس Rg وذلك لخفض استهلاك دارة القياس من الاستطاعة، ولزيادة الدقة، في حين إذا كانت حساسية المقياس غير كافية فيجب أن تساوي مقاومته المكافئة المقاومة الداخلية لمنبع القوة المحركة الكهربائية Rs بغية توفير الاستطاعة الكهربائية والحصول على أعظم حساسية عند القياس، ويتم الاعتماد على المبدأ نفسه عند قياس المقادير اللاكهربائية باستخدام تجهيزات القياس الكهربائية.
(الشكل -6) مخطط مقياس التدفق المغنطيسيوتستخدم المقاييس الغلفانية أيضاً لقياس التدفق المغنطيسي (السيالة المغنطيسية) وذلك بحذف عزم الإرجاع (النابض الميكانيكي) من تصميم الجهاز ورفده بوشيعة عيارية عدد لفاتها وسطح مقطعها محددان وتسمى عادة وشيعة الكاشف المغنطيسي (الشكل6).
عند وضع الوشيعة الكاشفة داخل الحقل المغنطيسي ينحرف مؤشر الجهاز بزاوية معينة بالنسبة للزاوية الابتدائية (صفر أو غير الصفر) وبمقدار متناسب طرداً مع التدفق المغنطيسي المجهول (السيالة المغنطيسية). وإن مقاييس التدفق المغنطيسي تعمل من دون آلية إرجاع المؤشر إلى الصفر، ويجري الإرجاع في العادة يدوياً بوساطة ذراع خاص، أو تحقق عملية القياس بتقدير قيمة الانحراف عن الوضع الابتدائي ويكون الفرق بين زاوية الانحراف قبل تأثير الحقل المغنطيسي وبعده هو القياس المطلوب.
وإن استخدام مقاومة التفريع مع مقاييس التدفق كما هي الحال في المقاييس الغلفانية يزيد من إمكانيات القياس ولكنه يسبب خفض حساسية الجهاز للتدفقات الصغيرة.
المقاييس التناسبية ذات الوشيعة المتحركة: تصمم المقاييس التناسبية بوجه عام من جميع أنواع المقاييس الكهرميكانيكية، وتقيس النسبة بين قيم مجهولة وأخرى عيارية معروفة داخل الجهاز لذلك تسمى بهذا الاسم. وتعتمد المقاييس التناسبية في مبدأ عملها على التجاوب بين تأثيرات المقادير الكهربائية في دخل الجهاز وعزمين قياسيين داخل الجهاز حيث تكون محصلة التأثير نتيجة تناسبية بين القيم الكهربائية المشاركة في العزمين. وفي أكثر الأحيان يعكس أحد العزمين التحسس بوجه مباشر في حين يعبر الآخر عن مقدار كهربائي عياري، وذلك لتسهيل إعداد الجهاز وتقليل أخطائه عند القياس. وتتكون المقاييس التناسبية عادة من وشيعتين متقاطعتين متحركتين على محور دوران مشترك، تولد الأولى عزم القياس وتولد الثانية عزماً معاكساً للأول يمثل عزم الإرجاع أي التوازن مع الأول. وتستعمل المقاييس التناسبية ذات الوشيعة المتحركة لقياس المقاومات (مقاييس الأوم التناسبية) وهي منتشرة بكثرة في الحياة العملية.
(الشكل -7) مخطط المقياس التناسبي
وعند مرور التيار الكهربائي في الوشيعة الأولى (الشكل 7) يتولد عزم القياس كما ذكر، ولكن عندما تكون وشيعتا الجهاز بلا نواة من الحديد المطاوع فإن الحقل المغنطيسي بين قطبي المغنطيس الدائم يكون منتظماً تقريباً، ولما كان التدفق المغنطيسي المخترق لسطح الوشيعة يتغير تغيراً جيبياً وكان عزم القياس هو عزم التوازن للوشيعة المتحركة الثانية فإن التدفق المغنطيسي فيه سيتغير كتابع جيب التمام.
وعندما تكون الزاوية بين الوشيعتين قائمة فإن معادلة التوازن تتعين من العلاقة:
حيث θ زاوية انحراف الجهاز، I1 و I2 التياران الماران في الوشيعتين الأولى والثانية، f التدفق المغنطيسي.
ويتضح من العلاقة الأخيرة أن ظل زاوية الانحراف يتناسب طرداً مع النسبة بين تياري الوشيعتين الأولى والثانية. فإذا كانت الزاوية (مقيسة بالراديان) صغيرة فإن ظلها يساويها تقريباً، وبهذه الطريقة يمكن قياس التناسب بين التيارات الكهربائية، وعندما يساوي تيار الوشيعة الثانية التيار الأسمى فيمكن قياس تيار الوشيعة الأولى، ولكن هذه الأجهزة لا تستخدم في قياس التيارات الكهربائية على الصعيد العملي لانعكاس جميع تغيرات منبع القوة المحركة الكهربائية أو التوتر على قيم التيارات المذكورة. وكذلك فإن نظام عمل الجهاز يعتمد على وشائع بلا نواة من الحديد المطاوع مما يؤدي إلى زيادة أبعاد الفجوة الهوائية للمغنطيس الدائم مما يسبب عدم انتظام الحقل المغنطيسي ومن ثم انخفاض الدقة في القياس.
وتستخدم المقاييس المغنطيسية التناسبية بوجه رئيسي بوصفها مقاييس أوم، أي عند ربط مقاومة عيارية مع الوشيعة الأولى ومقاومة مجهولة مع الوشيعة الثانية، فبحسب قانون أوم تتناسب التيارات ذات العلاقة مع قيم المقاومات ومن ثم يمكن تخفيف تأثير تغيرات التوتر المباشرة في عملية القياس، كما تحل مشكلة انتظام الحقل بوساطة نواة من الحديد المطاوع غير متناظرة لتوفير عزم القياس وعزم الإرجاع (الشكل 7).وبهذه الطريقة يمكن إنقاص طول الفجوة الهوائية واستخدام مولد يدوي للتيار المستمر لتأثيره الطفيف في سير عملية القياس.
(الشكل -8) مخطط المقياس المغنطيسي التناسبي
وإذا وضعت المقاومة على التسلسل في هذه المقاييس (الشكل 8) فيمكن قياس المقاومات الكبيرة ويسمى المقياس عندئذ مقياس الميغا أوم. ومن صفات هذا المقياس لوحته المعكوسة أي إن بدايته لانهائية، ونهايته تقابل الصفر. وإذا ربطت المقاومة على التفرع بوشيعتي المقياس فإن اللوحة تكون طبيعية أي أن زاوية الانحراف تتناسب طرداً مع المقاومة المجهولة ويسمى الجهاز عندئذ بمقياس الأوم للمقاومات الصغيرة.
أجهزة القياس الكهرديناميكية
تعتمد المقاييس الكهرديناميكية على التأثير المتبادل بين الحقلين المغنطيسيين لوشيعتين إحداهما ثابتة والثانية قابلة للحركة الدائرية في داخل الأولى، أي إن نشوء قوى كهرديناميكية داخل الجهاز يتبع تغيرات الطاقة المغنطيسية نتيجة التحريض المتبادل بين الوشيعتين، وإن المقاييس الكهرديناميكية متنوعة ومن أعمها المقياس ذو الوشيعة المتحركة الصغيرة الأبعاد التي توجد داخل وشيعة ثابتة مؤلفة من نصفين متساويين للحصول على حقل مغنطيسي منتظم (الشكل 9) ولتوفير انحراف المؤشر الميكانيكي على لوحة التدريج، والوشيعتان في هذا المقياس بلا نواة مغنطيسية لينة أي من الحديد المطاوع.
(الشكل 9) مخطط المقياس الكهرديناميكية
وهناك نماذج أخرى ذات نواة مغنطيسية لينة إلا أنها قليلة الاستخدام في الحياة العملية. وفي المقاييس الكهرديناميكية يتناسب عزم القياس طرداً مع جداء التيار الكهربائي المار في الوشيعة الأولى والتيار المار في الوشيعة الثانية وجيب التمام لزاوية فرق الطور بينهما، ويرتبط بتغيرات التحريض المتبادل بينهما الذي يمكن أن يأخذ مقداراً ثابتاً تقريباً عند اختيار أبعاد الوشيعتين الأولى والثانية اختياراً هندسياً دقيقاً.
ويتم التوازن داخل هذه الأجهزة بوساطة عزم نابض إرجاع ميكانيكي، ويمكن لهذه الأجهزة قياس المقادير الكهربائية المستمرة والمتناوبة.
ومن أهم أنواع هذه المجموعة مقاييس الأمبير والفولط والاستطاعة والمقاييس التناسبية ومقاييس التردد.
مقياس الأمبير الكهرديناميكي: يُراعى في هذا المقياس تحقيق بعض القيم النسبية بين أبعاد الوشيعتين الأولى والثانية، ومن أهمها أن تكون الوشيعة المتحركة ذات أبعاد صغيرة أي أن نصف قطر ناقلها دقيق أي أن تيارات تحميلها صغيرة.
(الشكل -10) مخطط مقياس الأمبير الكهرديناميكيولقياس التيار يجب أن تساوي زاوية فرق الطور بين التيار الأول والثاني الصفر وأن يتحقق التناسب الطردي بينهما وبين تيار الحمل. وعند قياس التيارات الصغيرة أي من مرتبة الملّي أمبير يمكن ربط الوشيعتين على التسلسل (الشكل 8) سواء أكان التيار مستمراً أم متناوباً لأن فرق الطور بين تياري الوشيعتين في هذه الحال يساوي الصفر، ولكن عند قياس تيارات من مرتبة أعلى تُستعمل الدارة المبينة في الشكل 10، أي باستخدام مقاومة أومية للتفريع بسبب عدم قدرة ناقل الوشيعة الداخلية على التحمل الحراري والديناميكي. وإذا كان التيار مستمراً فمن البدهي أن يكون متناسباً طرداً مع التيار المار في دخل المقياس. أما إذا كان متناوباً فيجب أن تكون زاوية فرق الطور بين التيارين الأول والثاني صفراً، ويتم ذلك أيضاً باختيار هندسي دقيق لمقاومة التفريع بالمقارنة بالممانعة التحريضية للوشيعة المتحركة. وفي حال تعذر ذلك تضاف ممانعة تحريضية صغيرة حتى يتم التوصل إلى المطلوب، أو تربط الوشيعة
الأولى على التسلسل مع مقاومة التفريع، وتربط الاثنتان معاً على التفرع مع ممانعة الوشيعة الثانية المتحركة.
مقياس الفولط الكهرديناميكي: وهو مقياس ملي كهرديناميكي تربط مقاومة أومية عالية أو عدة مقاومات (بحسب مجال قياس لوحة تدريجه) على التسلسل مع وشيعتيه.
وفي هذه الحالة، كما ذُكر سابقاً تتناسب زاوية انحراف الجهاز طرداً مع مقدار التوتر المطبق بين مربطيه، وتتميز المقاييس الكهرديناميكية لقياس التيار والتوتر بدقتها العالية وسهولة تصميمها وقلة استهلاكها من الاستطاعة.
(الشكل 11) مخطط مقياس الاستطاعة الكهرديناميكيمقياس الواط الكهرديناميكي: إن أكثر المقاييس انتشاراً في الحياة العملية هو مقياس الواط الكهرديناميكي الذي تتناسب زاوية انحرافه مع الاستطاعة الحقيقية للحمل، ولكي يتحقق ذلك فإن زاوية فرق الطور بين التيار في الوشيعة الثابتة والوشيعة المتحركة يجب أن تتناسب مع زاوية فرق الطور بين تيار الحمل وتوتره، إضافة إلى أن الوشيعة المتحركة يجب أن تمثل وشيعة توتر أومي، ولذلك تضاف مقاومة أومية عالية على التسلسل إلى الوشيعة المتحركة (الشكل 11) يكون مقدارها أكبر بكثير من مقدار ممانعة الوشيعة الثانية. ولهذا فإن عزم القياس يتناسب مع الاستطاعة الحقيقية، ومن ناحية أخرى يتناسب التيار المار في الوشيعة الثانية مع توتر الحمل ويطابقه بطوره.
ويربط مقياس الواط في دارة قياس الاستطاعة الحقيقية بطريقتين. فإما أن يقاس التيار أولاً من جهة التغذية ومن ثم يقاس التوتر وإما العكس. وفي الحالتين كلتيهما يرتكب خطأ في القياس، ففي الحالة الأولى يتوقف الخطأ على المقاومة الأومية لوشيعة التوتر، وفي الحالة الثانية ينتج الخطأ من المقاومة الأومية لوشيعة التيار (الوشيعة الأولى). ويتوقف اختيار الطريقة المناسبة على الاستطاعة الكهربائية للحمل.
(الشكل -12) مخطط مقياس عامل الاستطاعة: تتكون المقاييس الكهرديناميكية التناسبية من ثلاث وشائع: وشيعة ثابتة كما في المقاييس الكهرديناميكية العادية، ووشيعتين متحركتين إحداهما لتوليد عزم القياس كهربائياً والأخرى لتوليد عزم الإرجاع لتحقيق التوازن وبينهما زاوية معينة هي في أكثر الأحيان قائمة. وتستخدم المقاييس الكهرديناميكية التناسبية لقياس فرق الطور بين التيار والتوتر وتسمى مقياس الطور phase- meter. ولكن في أكثر الأحيان تدرج اللوحة بقيم جيب التمام لزاوية الطور لذلك تسمى مقاييس عامل الاستطاعة، ويبين (الشكل 12) مقياساً من هذا النوع. وفي هذا المقياس تربط الوشيعة الثابتة على التسلسل مع الحمل المراد قياس عامل استطاعته ويربط على التفرع مع الحمل الوشيعتان المتقاطعتان وتكون إحداهما مربوطة على التسلسل مع مقاومة أومية عالية في حين تكون الوشيعة الأخرى مربوطة مع مفاعلة تحريضية مقاومتها الأومية صغيرة، لهذا فإن التوتر المطبق على الحمل (توتر التغذية) يكوّن مع التيار المار في المقاومة الأومية فرقاً في الطور يساوي الصفر، على حين تكون زاوية تيار المفاعلة قريبة جداً من القائمة.
ويُصمم مقياس التردد الكهرديناميكي اعتماداً على نظرية المقاييس التناسبية من النوع المذكور، ولكن يربط مع الوشيعة المتحركة مفاعلة تحريضية ومع الوشيعة الأخرى المتقاطعة معها مفاعلة سَعَوِيَّة، ويعمل هذا المقياس اعتماداً على ظاهرة التجاوب بين المفاعلتين التحريضية والسعوية، أي إن الزاوية بين التيارين المارين في المفاعلتين هي قائمة ومن ثم فإن مربع التيار المار في الوشيعة الثابتة داخل المقياس يساوي مجموع مربعيهما، وتتوقف قيمته على قيمة المقاومة الأومية المكافئة داخل الجهاز (للوشائع الثلاث) باعتبار أن الممانعة التحريضية للوشيعة الثابتة صغيرة نسبياً.
ويساوي ظل زاوية الانحراف نسبة ظل زاوية فرق الطور بين التيار الكلي وتيار الوشيعة المتحركة الأولى إلى ظل زاوية فرق الطور بين التيار الكلي والتيار في الوشيعة المتحركة الثانية.
ولما كان ظل زاوية فرق الطور يتناسب مع المفاعلتين التحريضية والسعوية المتناسبتين مع التردد فإن الجهاز يمكن أن يستعمل لقياس التردد.
أجهزة القياس ذات النواة المتحركة
تعتمد أجهزة القياس ذات النواة المتحركة في مبدأ عملها على التأثير المتبادل بين الحقل المغنطيسي المتولد من تيار كهربائي مار في وشيعة ثابتة وبين الحقل المغنطسيسي لنواة من
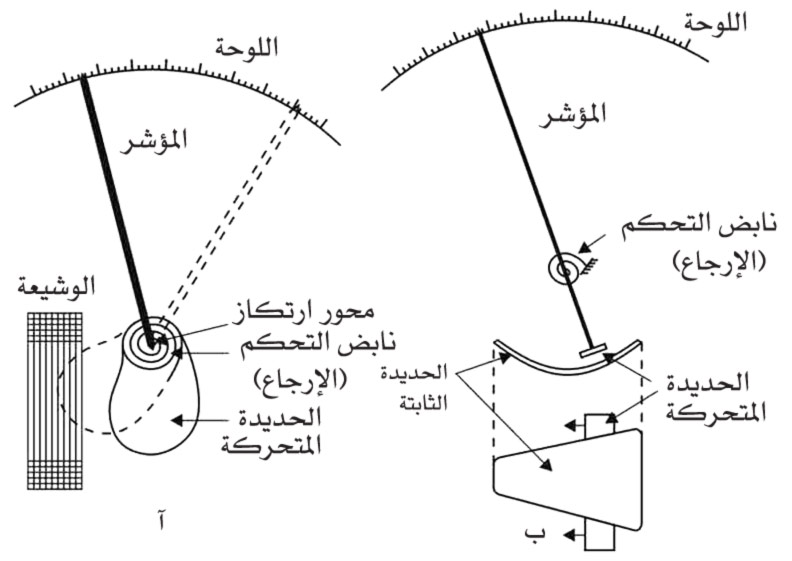(الشكل 13) مخطط المقياس ذي الحديدة المتحركة
الحديد المطاوع مثبتة على محور دوران الجهاز. وهناك نموذجان أساسيان معروفان لهذه الأجهزة: يسمى الأول بالنموذج التجاذبي (الشكل 13ـأ) ويتألف من وشيعة يمر فيها التيار المراد قياسه ومن حديدة منبسطة مثبتة لا مركزياً على محور عليه نابض الإرجاع والمؤشر، وعند مرور التيار يمغنط الحقل المغنطيسي الناتج الحديدة ويؤثر بقوى تجاذبية باتجاه التدفق المغنطيسي. أما النموذج الثاني فيسمى بالنموذج التنافري (الشكل 13 - ب) وهو وشيعة يثبت على جدارها الداخلي قطعة من الحديد المطاوع وقطعة أخرى مشابهة مثبتة على محور الدوران. وعند مرور التيار في الوشيعة الثابتة ينشأ حقل مغنطيسي باتجاه واحد مما يؤدي إلى مغنطة القطعتين الحديديتين الأولى والثانية بالقطبية المغنطيسية نفسها ويؤدي ذلك إلى ظهور قوى تنافرية تحدث عزم قياس يتوازن مع عزم نابض الإرجاع.
وتمتاز المقاييس الكهربائية ذات الحديدة المتحركة بسهولة تصميمها وبمتانتها الميكانيكية العالية، ولكن استهلاكها للاستطاعة الكهربائية كبير لكبر أبعاد وشائعها. وإضافة إلى ذلك فإن عزمها يتناسب مع مربع التيار أي يمكن أن تقاس قيم التيارات المستمرة كما تقاس القيم الفعالة للتيارات المتناوبة.
وهذه الأجهزة أقل دقة من المقاييس ذات الوشيعة المتحركة وأقل حساسية منها، لذلك تستخدم لقياس القيم الكبيرة للتيارات الكهربائية والقيم المتوسطة للتوترات. ولكن أبرز سلبياتها هو تأثرها الشديد بترددات التيارات المقيسة التي تسبب زيادة الممانعة التحريضية الداخلية لذلك تعمل ضمن مجال ترددي ضيق لا يمكن توسيعه إلا بالطرائق الكهربائية وضمن حدود كيلو هرتز فقط.
أجهزة القياس الرقمية
تتميز أجهزة القياس الرقمية بالمقارنة بالمقاييس التمثيلية، بعدة إيجابيات مهمة هي: الدقة العالية، والسرعة الكبيرة في القياس، وإعطاء النتيجة على شكل أرقام جاهزة، وإمكانية تنظيم عملها مع الذاكرة والحواسيب، وتحقيق القياس عن بعد بسهولة. لذلك انتشرت هذه الأجهزة بسرعة كبيرة في الحياة العملية القياسية.
وتعتمد أجهزة القياس الرقمية في مبدأ عملها على تقطيع الإشارة المراد قياسها زمنياً لأخذ العينات التي يجب أن تتميز بالخصائص الثلاث التالية: أن تعبّر تكاملياً عن المقدار المراد قياسه، وأن تتضمن مواصفاته كافة، وأن تكون صالحة تقنياً للتطبيق على مدخل الجهاز. وبعد أخذ العينة القياسية يقوم الجهاز الرقمي بتحقيق عملية التَكْمِيَة quantization (مضاعفات لِكَمٍّ معين في زمن محدد) ومن ثم تحقيق القياس بوساطة عداد ثنائي - عشري بعد عملية التَّرميز coding وإظهار النتيجة رقمياً عن طريق شاشة مضيئة.
وإن أبسط مقدار يقاس رقمياً هو الزمن بوساطة هزاز oscillator دور اهتزازاته ثابت، وشكلها جيبي أو نبضي، وعددها يمثل الزمن أو التردد. ولهذا السبب فإن أبسط طرائق قياس المقادير الكهربائية رقمياً هي التي تعتمد على التبديل الترددي أو الزمني للمقدار نفسه. ويمكن استخدام طرائق المقارنة بقيم مشابهة ولكنها أكثر تعقيداً ولها سلبياتها ولاسيما فيما يتعلق بأخطاء القياس.
ويستخدم أكثر مقاييس الفولط الرقمية لقياس التوترات المستمرة بسبب سهولة أخذ العينة ومعالجتها. ولكي تقاس التوترات رقمياً يجب تقطيعها إلى عينات بوساطة المبدل التمثيلي - الرقمي وتبعاً لمبدأ عمل هذا المبدِّل تصنف مقاييس الفولط الرقمية في الأنواع التالية:
مقاييس الفولط الرقمية ذات التقريب المتتابع: تعتمد مقاييس الفولط الرقمية ذات التقريب المتتابع في مبدأ عملها على استعمال مبدلات تمثيلية - رقمية من نوع ذات التقريب المتتالي. أما طريقة التقريب المتتالي فتماثل عملية القسمة العشرية والثنائية إذ تتم مقارنة التوتر المراد قياسه بتوتر مرجعي معروف أولاً ثم مقارنة الباقي بأجزاء من هذا التوتر المرجعي مثل
1 ، 1 ، 1 ،....
2 4 8
وبهذه الطريقة يتم إعطاء القيمة الرقمية المناسبة للتوتر المقيس. أما بنية هذه المقاييس فهي كما في الشكل 14.
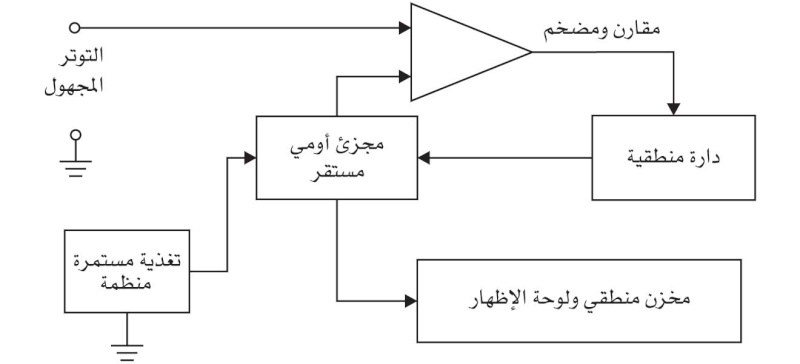(الشكل 14) مخطط مقياس الفولط الرقميمقاييس الفولط الرقمية ذات الميل الأحادي: تعتمد مقاييس الفولط الرقمية ذات الميل الأحادي في مبدأ عملها على تقنية تبديل التوتر بالزمن. أما عملها فيمكن إيجازه على الوجه الآتي:
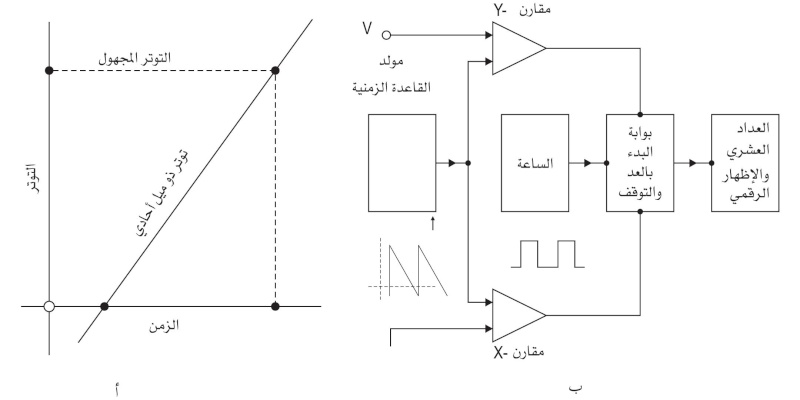(الشكل 15) مخطط مقياس الفولط الرقمي ذي الميل الأحادي
يطبق التوتر الثابت المراد قياسه على عنصر تكاملي فيكون خرجه تابعاً خطياً للزمن ramp function. وبعد ذلك تجري مقارنة التابع الخطي بتوتر مرجعي معروف. ويبقى خرج هذا المقارن مساوياً للواحد إلى أن يتساوى التوتران المرجعي والمقيس. بعد ذلك يعود الخرج للصفر. أي أن خرج المقارن هو نبضة ذات عرض محدد. وبقياس هذا الزمن، أي عرض النبضة، يمكن معرفة قيمة التوتر المراد قياسه (الشكل 15).
مقاييس الفولط الرقمية ذات الميل المضاعف: تعتمد هذه الأجهزة على مبدأ المقاييس ذات الميل الأحادي نفسه ألا وهو تبديل التوتر بالزمن ومن ثم قياس هذا الزمن رقمياً. وتمتاز بأنها أكثر دقة من المقاييس ذات الميل الأحادي لأنها تحقق القياس على الميلين (الشكل 16).
(الشكل 16) مخطط مقياس الفولط الرقمي ذي الميلينمقاييس الفولط الرقمية ذات تبديل التوتر بالتردد: تعتمد مقاييس الفولط الرقمية ذات تبديل التوتر بالتردد في عملها على استخدام مبدلات تمثيلية - رقمية تحول التوتر المراد قياسه إلى تردد وذلك بوساطة هزاز نبضي ذي دور ثابت ويتحكم هذا الهزاز في بوابة منطقية AND gate تعمل صِمَامَ فتح وإغلاق. وعندما تفتح البوابة بتأثير الهزاز تشحن مكثفة بالإشارة المرجعية. وبعد أن تزول نبضة الهزاز تغلق البوابة مؤدية إلى تفريغ شحنة المكثفة أو شحنها بالاتجاه المعاكس بتأثير التوتر المقيس. وينتج من عملية الشحن والتفريغ هذه إشارة ذات تردد تابع لقيمة التوتر المقيس.
وتمكِّن معرفة تردد هذه الإشارة، بوساطة عدّ النبضات المعيارية للهزاز خلال الدور من معرفة التوتر المقيس (الشكل 17).
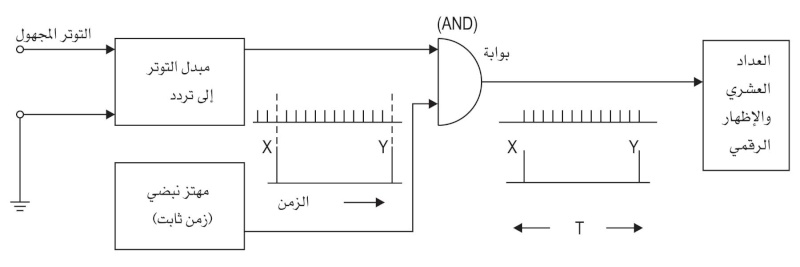(الشكل 17) مخطط مقياس الفولط الرقمي الذي يستبدل التردد بالتوتر المراد قياسه
موضوع: أدوات القياس الكهربائية 
السبت 17 أكتوبر - 5:54
