[size=24]1. How do you convert a XOR gate into a buffer and a inverter (Use only one XOR gate for each)?

2. Implement an 2-input AND gate using a 2x1 mux.

3. What is a multiplexer?
A multiplexer is a combinational circuit which selects one of many input signals and directs to the only output.
4. What is a ring counter?
A
ring counter is a type of counter composed of a circular shift
register. The output of the last shift register is fed to the input of
the first register. For example, in a 4-register counter, with initial
register values of 1100, the repeating pattern is: 1100, 0110, 0011,
1001, 1100, so on.
5. Compare and Contrast Synchronous and Asynchronous reset.
Synchronous
reset logic will synthesize to smaller flip-flops, particularly if the
reset is gated with the logic generating the d-input. But in such a
case, the combinational logic gate count grows, so the overall gate
count savings may not be that significant. The clock works as a filter
for small reset glitches; however, if these glitches occur near the
active clock edge, the Flip-flop could go metastable. In some designs,
the reset must be generated by a set of internal conditions. A
synchronous reset is recommended for these types of designs because it
will filter the logic equation glitches between clock.
Problem with
synchronous resets is that the synthesis tool cannot easily distinguish
the reset signal from any other data signal. Synchronous resets may
need a pulse stretcher to guarantee a reset pulse width wide enough to
ensure reset is present during an active edge of the clock, if you have
a gated clock to save power, the clock may be disabled coincident with
the assertion of reset. Only an asynchronous reset will work in this
situation, as the reset might be removed prior to the resumption of the
clock. Designs that are pushing the limit for data path timing, can not
afford to have added gates and additional net delays in the data path
due to logic inserted to handle synchronous resets.
Asynchronous
reset: The major problem with asynchronous resets is the reset release,
also called reset removal. Using an asynchronous reset, the designer is
guaranteed not to have the reset added to the data path. Another
advantage favoring asynchronous resets is that the circuit can be reset
with or without a clock present. Ensure that the release of the reset
can occur within one clock period else if the release of the reset
occurred on or near a clock edge then flip-flops may go into metastable
state.
6. What is a Johnson counter?
Johnson
counter connects the complement of the output of the last shift
register to its input and circulates a stream of ones followed by zeros
around the ring. For example, in a 4-register counter, the repeating
pattern is: 0000, 1000, 1100, 1110, 1111, 0111, 0011, 0001, so on.
8. In a 4-bit Johnson counter How many unused states are present?
4-bit Johnson counter: 0000, 1000, 1100, 1110, 1111, 0111, 0011, 0001, 0000.
8 unused states are present.
9. Design a 3 input NAND gate using minimum number of 2 input NAND gates.

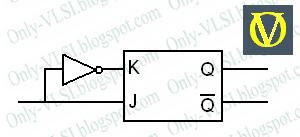
10. How can you convert a JK flip-flop to a D flip-flop?
Connect the inverted J input to K input.
11. What are the differences between a flip-flop and a latch?
Flip-flops are edge-sensitive devices where as latches are level sensitive devices.
Flip-flops are immune to glitches where are latches are sensitive to glitches.
Latches require less number of gates (and hence less power) than flip-flops.
Latches are faster than flip-flops.
12. What is the difference between Mealy and Moore FSM?
Mealy
FSM uses only input actions, i.e. output depends on input and state.
The use of a Mealy FSM leads often to a reduction of the number of
states.
Moore FSM uses only entry actions, i.e. output depends only
on the state. The advantage of the Moore model is a simplification of
the behavior.
13. What are various types of state encoding techniques? Explain them.
One-Hot encoding:
Each state is represented by a bit flip-flop). If there are four states
then it requires four bits (four flip-flops) to represent the current
state. The valid state values are 1000, 0100, 0010, and 0001. If the
value is 0100, then it means second state is the current state.
One-Cold encoding:
Same as one-hot encoding except that '0' is the valid value. If there
are four states then it requires four bits (four flip-flops) to
represent the current state. The valid state values are 0111, 1011,
1101, and 1110.
Binary encoding: Each state is represented by a binary code. A FSM having '2 power N' states requires only N flip-flops.
Gray encoding: Each state is represented by a Gray code. A FSM having '2 power N' states requires only N flip-flops.
14. Define Clock Skew , Negative Clock Skew, Positive Clock Skew.
Clock
skew is a phenomenon in synchronous circuits in which the clock signal
(sent from the clock circuit) arrives at different components at
different times. This can be caused by many different things, such as
wire-interconnect length, temperature variations, variation in
intermediate devices, capacitive coupling, material imperfections, and
differences in input capacitance on the clock inputs of devices using
the clock.
There are two types of clock skew: negative skew and
positive skew. Positive skew occurs when the clock reaches the
receiving register later than it reaches the register sending data to
the receiving register. Negative skew is the opposite: the receiving
register gets the clock earlier than the sending register.
15. Give the transistor level circuit of a CMOS NAND gate.

16. Design a 4-bit comparator circuit.
17. Design a Transmission Gate based XOR. Now, how do you convert it to XNOR (without inverting the output)?
18. Define Metastability.
If
there are setup and hold time violations in any sequential circuit, it
enters a state where its output is unpredictable, this state is known
as metastable state or quasi stable state, at the end of metastable
state, the flip-flop settles down to either logic high or logic low.
This whole process is known as metastability.
19. Compare and contrast between 1's complement and 2's complement notation.
The
only advantage of 1's complement is that it can be calculated easily,
just by changing 0's into 1's and 1's into 0's. The 2's complement is
calculated in two ways, (i) add 1 to the 1's complement of the number,
and (ii) leave all the leading 0s in the least significant positions
and keep first 1 unchanged, and then change 0's into 1's and 1's into
0's.
The advantages of 2's complement over 1's complement are:
(i)
For subtraction with complements, 2's complement requires only one
addition operation, where as for 1's complement requires two addition
operations if there is an end carry.
(ii) 1's complement has two arithmetic zeros, all 0's and all 1's.
20. Give the transistor level circuit of CMOS, nMOS, pMOS, and TTL inverter gate.

21. What are set up time and hold time constraints?
Set
up time is the amount of time before the clock edge that the input
signal needs to be stable to guarantee it is accepted properly on the
clock edge.
Hold time is the amount of time after the clock edge
that same input signal has to be held before changing it to make sure
it is sensed properly at the clock edge.
Whenever there are setup
and hold time violations in any flip-flop, it enters a state where its
output is unpredictable, which is known as as metastable state or quasi
stable state. At the end of metastable state, the flip-flop settles
down to either logic high or logic low. This whole process is known as
metastability.
22. Give a circuit to divide frequency of clock cycle by two.

23. Design a divide-by-3 sequential circuit with 50% duty circle.
24. Explain different types of adder circuits.
25. Give two ways of converting a two input NAND gate to an inverter.

26. Draw a Transmission Gate-based D-Latch.
27. Design a FSM which detects the sequence 10101 from a serial line without overlapping.
28. Design a FSM which detects the sequence 10101 from a serial line with overlapping.
29. Give the design of 8x1 multiplexer using 2x1 multiplexers.
30. Design a counter which counts from 1 to 10 ( Resets to 1, after 10 ).
31. Design 2 input AND, OR, and EXOR gates using 2 input NAND gate.

32. Design a circuit which doubles the frequency of a given input clock signal.
33. Implement a D-latch using 2x1 multiplexer(s).

34. Give the excitation table of a JK flip-flop.
35. Give the Binary, Hexadecimal, BCD, and Excess-3 code for decimal 14.
14:
Binary: 1110
Hexadecimal: E
BCD: 0001 0100
Excess-3: 10001
36. What is race condition?
37. Give 1's and 2's complement of 19.
19: 10011
1's complement: 01100
2's complement: 01101
38. Design a 3:6 decoder.
39. If A*B=C and C*A=B then, what is the Boolean operator * ?
* is Exclusive-OR.
40. Design a 3 bit Gray Counter.
41. Expand the following: PLA, PAL, CPLD, FPGA.
PLA - Programmable Logic Array
PAL - Programmable Array Logic
CPLD - Complex Programmable Logic Device
FPGA - Field-Programmable Gate Array
42. Implement the functions: X = A'BC + ABC + A'B'C' and Y = ABC + AB'C using a PLA.

43. What are PLA and PAL? Give the differences between them.
Programmable Logic Array is a programmable device used to implement
combinational logic circuits. The PLA has a set of programmable AND
planes, which link to a set of programmable OR planes, which can then
be conditionally complemented to produce an output.
PAL is
programmable array logic, like PLA, it also has a wide, programmable
AND plane. Unlike a PLA, the OR plane is fixed, limiting the number of
terms that can be ORed together.
Due to fixed OR plane PAL allows
extra space, which is used for other basic logic devices, such as
multiplexers, exclusive-ORs, and latches. Most importantly, clocked
elements, typically flip-flops, could be included in PALs. PALs are
also extremely fast.
44. What is LUT?
- Look-Up Table. An n-bit look-up table can be implemented with a
multiplexer whose select lines are the inputs of the LUT and whose
inputs are constants. An n-bit LUT can encode any n-input Boolean
function by modeling such functions as truth tables. This is an
efficient way of encoding Boolean logic functions, and LUTs with 4-6
bits of input are in fact the key component of modern FPGAs.
45. What is the significance of FPGAs in modern day electronics? (Applications of FPGA.)
- ASIC
prototyping: Due to high cost of ASIC chips, the logic of the
application is first verified by dumping HDL code in a FPGA. This helps
for faster and cheaper testing. Once the logic is verified then they
are made into ASICs.
- Very useful in applications that can make
use of the massive parallelism offered by their architecture. Example:
code breaking, in particular brute-force attack, of cryptographic
algorithms.
- FPGAs are sued for computational kernels such as FFT or Convolution instead of a microprocessor.
- Applications
include digital signal processing, software-defined radio, aerospace
and defense systems, medical imaging, computer vision, speech
recognition, cryptography, bio-informatics, computer hardware emulation
and a growing range of other areas.
46. What are the differences between CPLD and FPGA.
47. Compare and contrast FPGA and ASIC digital designing.
48. Give True or False.
(a) CPLD consumes less power per gate when compared to FPGA.
(b) CPLD has more complexity than FPGA
(c) FPGA design is slower than corresponding ASIC design.
(d) FPGA can be used to verify the design before making a ASIC.
(e) PALs have programmable OR plane.
(f) FPGA designs are cheaper than corresponding ASIC, irrespective of design complexity.
Answer(a) False
(b) False
(c) True
(d) True
(e) False
(f) False
49. Arrange the following in the increasing order of their complexity: FPGA,PLA,CPLD,PAL.
Increasing order of complexity: PLA, PAL, CPLD, FPGA.
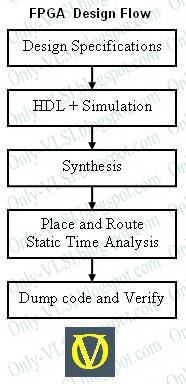
50. Give the FPGA digital design cycle.
51. What is DeMorgan's theorem?
For N variables, DeMorgan’s theorems are expressed in the following formulas:
(ABC..N)' = A' + B' + C' + ... + N' -- The complement of the product is equivalent to the sum of the complements.
(A + B + C + ... + N)' = A'B'C'...N' -- The complement of the sum is equivalent to the product of the complements.
This relationship so induced is called DeMorgan's duality.
52. F'(A, B, C, D) = C'D + ABC' + ABCD + D. Express F in Product of Sum form.
Complementing both sides and applying DeMorgan's Theorem:
F(A, B, C, D) = (C + D')(A' + B' + C)(A' + B' + C' + D')(D')
53. How many squares/cells will be present in the k-map of F(A, B, C)?
F(A, B, C) has three variables/inputs.
Therefore, number of squares/cells in k-map of F = 2(Number of variables) = 23 = 8.
54. Simplify F(A, B, C, D) = S ( 0, 1, 4, 5, 7, 8, 9, 12, 13)
The four variable k-map of the given expression is:
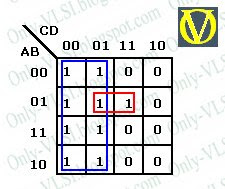
The grouping is also shown in the diagram. Hence we get,
F(A, B, C, D) = C' + A'BD
55. Simplify F(A, B, C) = S (0, 2, 4, 5, 6) into Product of Sums.
The three variable k-map of the given expression is:

The 0's are grouped to get the F'.
F' = A'C + BC
Complementing both sides and using DeMorgan's theorem we get F,
F = (A + C')(B' + C')
56. The simplified expression obtained by using k-map method is unique. True or False. Explain your answer.
False. The simplest form obtained is not necessarily unique as grouping can be made in different ways.
57. Give the characteristic tables of RS, JK, D and T flip-flops.
RS flip-flop.
JK flip-flop
| J | K | Q(t+1) |
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q'(t) |
D flip-flop
T flip-flop
58. Give excitation tables of RS, JK, D and T flip-flops.
RS flip-flop.
| Q(t) | Q(t+1) | S | R |
| 0 | 0 | 0 | X |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | X | 0 |
JK flip-flop
| Q(t) | Q(t+1) | J | K |
| 0 | 0 | 0 | X |
| 0 | 1 | 1 | X |
| 1 | 0 | X | 1 |
| 1 | 1 | X | 0 |
D flip-flop
T flip-flop
59. Design a BCD counter with JK flip-flops
60. Design a counter with the following binary sequence 0, 1, 9, 3, 2, 8, 4 and repeat. Use T flip-flops.

